1.目的
1. 共鳴現象の理解
試験管内の空気が音と共鳴することで、大きな音が発生することを体験できます。
この実験を通じて、共鳴とは特定の振動数で振動が増幅される現象であることを実感できます。
2. 定常波と波長の関係の理解
試験管内では、開口端と閉口端で異なる境界条件により定常波が形成されます。
このとき、波長と試験管の長さの関係を学ぶことで、物理の基本である「波の性質」を深く理解できます。
3. 音の速さの測定
気柱の長さと共鳴する振動数を測定することで、空気中の音速を求めることができます。これは、物理法則を実験で確かめる経験となります。
4. 応用への理解
気柱共鳴は楽器の音の仕組みに関連しています。理論だけでなく、実際の楽器や音響技術に応用される現象を学ぶことができます。
5. 実験による探究的学習
試験管の長さを変えたり、水を用いて有効な管の長さを調整したり、実験的にデータを取り、物理の法則を確認する経験ができます。
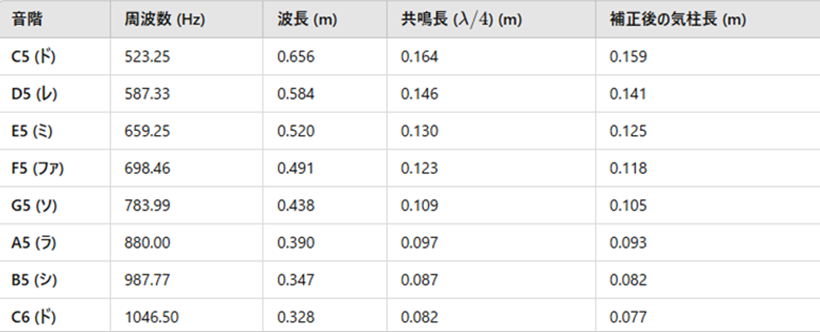
2.気柱共鳴のしくみ気柱の長さと振動数
気柱共鳴の原理を使って、試験管に水を入れた場合の音階ごとの水面から口までの長さを計算できます。この計算では、以下の条件を仮定します。
1.音速 (v):v=343 m/s(気温20℃の空気中の音速)
2.開管の条件: 試験管の片方は開口しており、もう片方は水面で閉じています。これにより、閉管共鳴が成立します。
閉管共鳴の公式
閉管の場合、共鳴の基本波長 (λ) は試験管の長さ (L) と関係します。基本振動において、閉管の長さは波長の 4分の1 に相当します。
L=λ/4
波長と周波数 (f) の関係式は次の通りです:
λ=v/f
これを利用して、音階ごとの試験管の長さ L を計算します。
計算手順
1.各音階の周波数(f)を使って波長(λ)を計算します:
λ=v/f
2.波長を元に試験管の長さ(L)を計算します:
L=λ/4
計算方法の例
ド(C4)の場合:
1.波長:
λ=343/261.63 ≈ 1.312m
2.試験管の長さ:
L=λ/4 ≈ 0.328m
他の音階も同様に計算しています。
試験管の条件:
・試験管の長さ:18cm(Leff=0.18m)
・試験管の内径:16mm(r=8mm=0.008m)
・開口端補正:e=0.6・r=0.6・0.008=0.0048m
補正後の長さ
試験管の有効共鳴長は次の式で計算します:
L=Leff-e
試験管のパラメータ
・試験管の長さ:18cm(Leff=0.18m)
・開口端補正:e=0.0048m
・有効共鳴長:Lactual=0.1752m
計算結果(C5~C6)
C5からC6の範囲で、試験管の長さ(18cm=0.18m)を超えない範囲で共鳴できる音階を確認しました。
3.準備
使用する製品
E31-8200-14 ワイヤレス音センサ GDX-SND(Go Direct)
用意するもの
パソコンまたはスマホ、ノギス(または定規)
器具:試験管18cm、ストロー、ビーカー100mL、スポイト、水、試験管たて、棒温度計
4.実験の手順
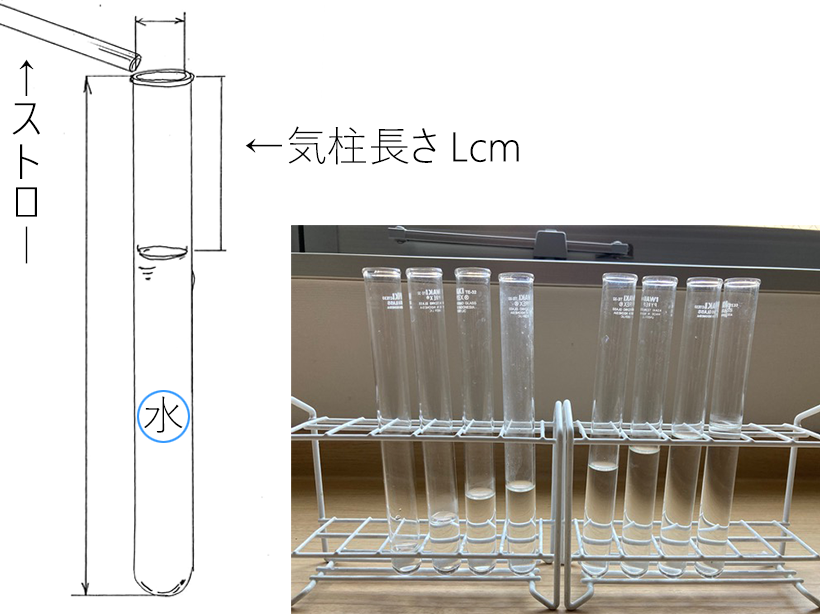
1.試験管に水を入れて、所定の長さの気柱になるように、水を注ぎます。
2.試験管の気柱の高さは、およそ18mmでストローを試験管の口につけ、ストローを軽くふいて、音を出します。 直接、試験管に口をつけないでください。

3.音センサで音をひろい、タブレットPCにつなぎ記録します。そして、振動数fを数えます。
4.ねらいの音階の振動数になったら、試験管の気柱を記録します。気柱の長さは水滴で1~2敵でも敏感に変わります。
実験のコツ:ストローは試行錯誤で音が出ます。ストローで軽くふく方がきれいな共鳴が起きます。
5.実験結果
<開口端補正の長さで測定>
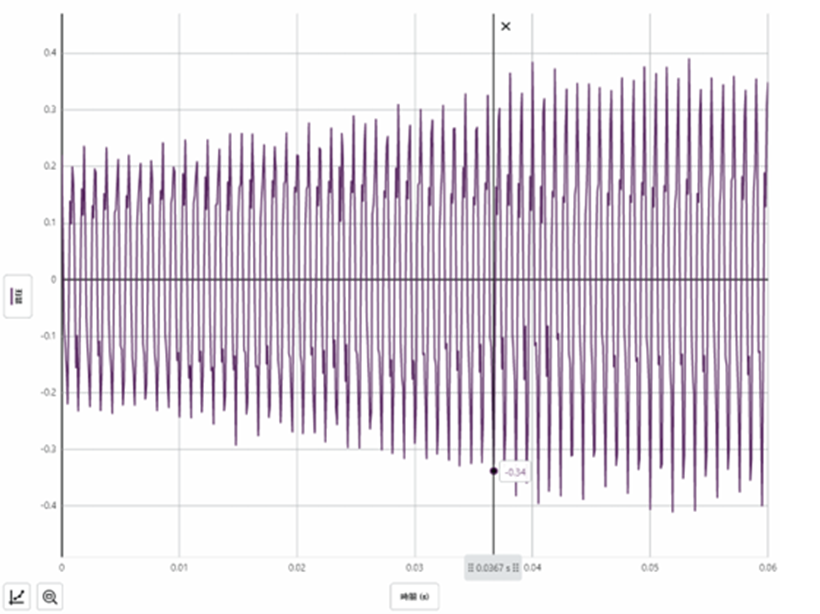
音階 ド(C5)
理想 振動数 f=523Hz 気柱長さL=15.9㎝ 気温22℃
結果 共鳴した振動数 f=26.1/0.05=522Hz 気柱長さ L=15.7cm (有効補正長さ)
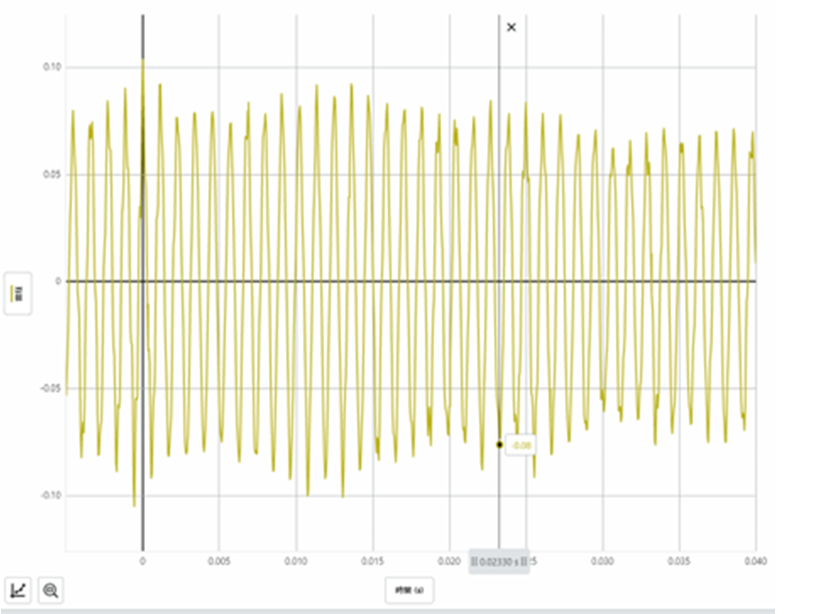
音階 ラ(A5)
理想 共鳴する振動数 f=880Hz 気柱の長さ L=9.30㎝ 気温22℃
結果 共鳴した振動数 f=44/0.05=882Hz 気柱の長さ L=9.62cm (有効補正長さ)
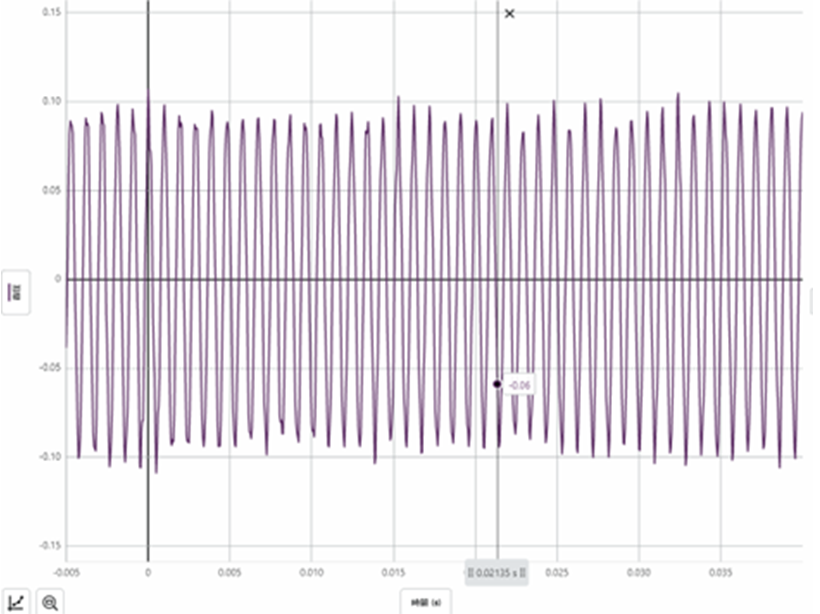
音階 ド(C6)
理想 振動数 1047Hz 気柱の長さ L=7.70㎝ 気温22℃
結果 共鳴した振動数 1047.5Hz 気柱の長さ L=7.76㎝ (有効補正長さ)
